水道方式について

タイルを見て、触れて、五感で楽しく体感しながら、数が持つ「量」を学びます。数という抽象と、具体物を結ぶのが、半具体物のタイルです。数の入門から、たし算・ひき算、かけ算・わり算、小数、分数までタイル操作をして量を体得します。また、速さ・密度・濃度といった目に見えない「単位当たり量」からは、タイル操作で得たイメージを基にタイル図を書いて学びを積み上げていきます。水道方式は、子どもたちに分かりやすいタイルと教具を駆使し、算数ゲーム、工作など、実体験に基づく楽しい学びを実践しています。
すべての子どもに「わかる算数 」を
1958年、水道方式の礎を築いたのは東京工業大学教授の遠山 啓氏でした。算数が苦手な子にも、算数が得意な子にも、わかる指導法はひとつであることを提唱し数学教育協議会を立ち上げ、世界の教科書を研究し理論的に体系立てたのが水道方式の算数です。すべての子どもに分かる算数として、今も多くの指導者に引き継がれ研究実践が行われています。小学校の教科書にタイルが導入されたのも、その分かりやすさが所以です。まさにユニバーサルデザインの指導法が半世紀も前に生み出されていたのです。
根源教育としての障害児教育
障害児に教科教育の道筋を作ったのも遠山啓氏です。当時、八王子養護学校で自らが指導者として水道方式の算数の実践をし、子どもたちの様々な示唆を受け人間観・教育観の原点に出会います。「子供に学びの意欲を起こさせるための正しい方法は、学問や芸術の本来のおもしろさ、底知れない深遠さ、複雑さを子どもたちに味わわせることであり、それ以外にあり得ない」それが遠山氏のゆるぎない信念でした。
水道方式の特徴
- 量に基づく 集合数を数の基本にすえて指導します。
- タイルを使う 量に基づき数を捉える時、タイルが数と具体物の仲立ちとな ります。
- 筆算を重視する 横書きの暗算重視ではなく、各位ごとに足す縦書きを重視し ます。
- 分析と総合 3ケタたす3ケタのたし算だけでも81万題。すべての計算問題 を型分けし、典型的な型を解けるようにすれば、すべてが解 けることになります。
この原則に沿いながら、算数・数学のあらゆる分野にわたり絶えざる実践と研究を重ね、すべての子どもたちに分かる質の高いさんすう・数学教育を目指しています。
タイルの意味

量に基づいて数を捉えるとき、その仲立となるのがタイルです。タイルは数の概念を視覚的に捉えることを可能にします。算数の入門期に最も重要なのは算用数字の仕組みを理解することです。算用数字は、十進法と位取りから成り立っています。 タイルは正方形ですから、1を10個つなぐと、1本の連結した長い棒になり、更にそれを10本つなぐと、1枚の広い正方形となります。
このように、タイルは10・100・・・を1束としてとらえられ、量を明確に表現できる優れた教具なのです。子どもたちは、このタイルを手で操作しながら量のイメージを容易につかめるようになります。 ➡ タイルのおうちゲーム
「さんすうのおうち」
十進位取記数法を指導するための教具です。

タイルの教具

千のくらいまでの十進位取りボード ➡

かずの階段 数を量でとらえる教具

こんなたし算もタイルがあれば簡単!

さんすうのおうち
十の位までの位取りシート&タイル
繰り上がり・繰り下がりゲーム用にも

かけわりボード
かけ算わり算の意味を、具体物とタイルで学びます。

5の合成分解・10の合成分解
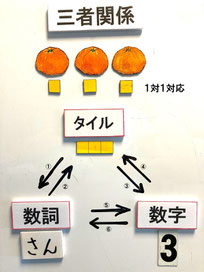
数がわかるということ

5までの合成分解